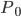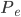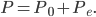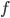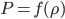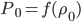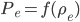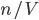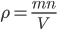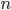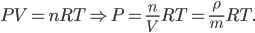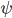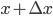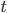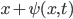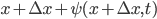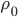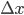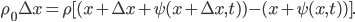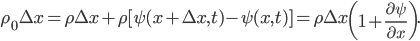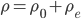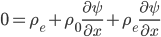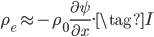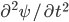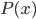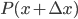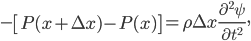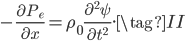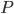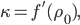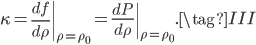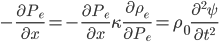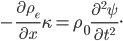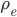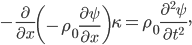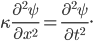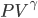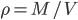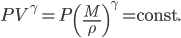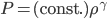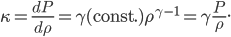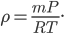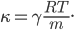The other day, my wife cooked up some microwavable popcorn while I was down the hall in the bedroom. The sound of the popcorn being made traveled seemingly instantly, but it took a full 5 minutes before the buttery smell came down the hall. Why is one so slow and the other so fast? Both of these rates have something to do with the air. But what?
By now we have a pretty good picture of what is happening in a gas. There are about 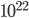 or so gas molecules in every cubic centimeter. These are flying around at relatively high speeds, and the average speed is something like
or so gas molecules in every cubic centimeter. These are flying around at relatively high speeds, and the average speed is something like 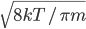 , or about 500 m/s (about 1100 miles per hour) at room temperature. That is fast...damn fast! Yet somehow the aromatic molecules coming off the popcorn take 5 whole minutes to traverse the approximately 10 meters from the microwave to the bedroom.
, or about 500 m/s (about 1100 miles per hour) at room temperature. That is fast...damn fast! Yet somehow the aromatic molecules coming off the popcorn take 5 whole minutes to traverse the approximately 10 meters from the microwave to the bedroom.
Of course, the answer is that the molecules are constantly running into each other. If there were no gas in between the microwave and the bedroom, the molecule would get there in 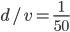 s. But as they try to make their way, they collide with all of the molecules around them, and this makes them bounce off in all sorts of directions. They do eventually make it, but it takes quite awhile.
s. But as they try to make their way, they collide with all of the molecules around them, and this makes them bounce off in all sorts of directions. They do eventually make it, but it takes quite awhile.
Let's come up with some quantities that would be useful in thinking about this. A molecule in a gas at temperature  experiences a lot of collisions every second. Let's call
experiences a lot of collisions every second. Let's call 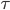 (that's tau) the mean time between collisions. As an unrealistic example, if a molecule experiences 50 collisions in 10 seconds, the mean collision time is 0.2 s. That's the average time for a molecule to go without running into anything. In air at room temperature this time is about
(that's tau) the mean time between collisions. As an unrealistic example, if a molecule experiences 50 collisions in 10 seconds, the mean collision time is 0.2 s. That's the average time for a molecule to go without running into anything. In air at room temperature this time is about 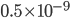 seconds, or 0.5 nanoseconds. That doesn't mean that every molecule goes that long before colliding. Sometimes a molecule will collide much sooner, and sometimes much later. But on average, that's the time.
seconds, or 0.5 nanoseconds. That doesn't mean that every molecule goes that long before colliding. Sometimes a molecule will collide much sooner, and sometimes much later. But on average, that's the time.
There is also the average distance that the molecule travels before running into another molecule, called the mean free path, 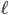 . The gas molecules are separated by only about 3.3 nanometers, so you might thinking that the mean free path is around that value. But amazingly, the mean free path is about 93 nm. The gas molecules travel much farther than one would think before running into something. Imagine standing in a room where there are 3 ft separating you from everybody else on average, everyone walking around and bumping into each other. Then imagine I told you that if you started walking in one direction, you would travel 93 feet without running into somebody. Crazy! But gas molecules are so small, and the forces so short ranged, compared to the spacing between them that it's true. This is why I say that molecules in a gas don't run into each other very often: compared with a liquid they travel a really long distance before running into something.
. The gas molecules are separated by only about 3.3 nanometers, so you might thinking that the mean free path is around that value. But amazingly, the mean free path is about 93 nm. The gas molecules travel much farther than one would think before running into something. Imagine standing in a room where there are 3 ft separating you from everybody else on average, everyone walking around and bumping into each other. Then imagine I told you that if you started walking in one direction, you would travel 93 feet without running into somebody. Crazy! But gas molecules are so small, and the forces so short ranged, compared to the spacing between them that it's true. This is why I say that molecules in a gas don't run into each other very often: compared with a liquid they travel a really long distance before running into something.
Suppose we focus in on two imaginary boxes in the air. Box 1 has 9 "special" molecules (solid circles) among its around 25 "normal" molecules (empty circles). Box 2 has only 3 special molecules for the same amount of air. This is not an equilibrium condition. Randomly, the special molecules will travel to the right to even things out. This tendency is called diffusion. The special molecules in box 1 can travel to the right past the imaginary wall. However, note that the special molecules in box 2 can also jump back into box 1. It's just more likely that the ones from box 1 will jump to box 2, since there are more of them.
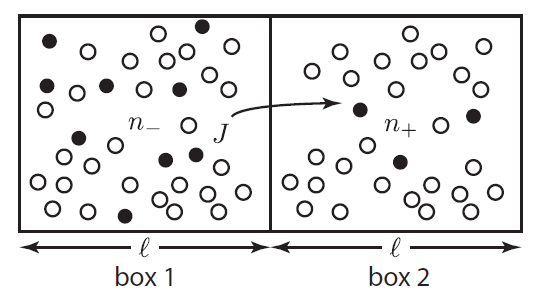 The net rate of flow of molecules from box 1 to box 2 we call
The net rate of flow of molecules from box 1 to box 2 we call 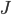 . It will depend, obviously, on how many special molecules there are. Let's call the number of special molecules in box 1 (per unit volume)
. It will depend, obviously, on how many special molecules there are. Let's call the number of special molecules in box 1 (per unit volume) 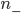 and the number in box 2
and the number in box 2 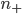 . You notice that the boxes in the picture are of a size
. You notice that the boxes in the picture are of a size 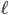 , the mean free path. That means that during a time
, the mean free path. That means that during a time 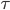 , on average
, on average 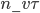 will cross the imaginary barrier from the left to the right, since the distance they can travel is about
will cross the imaginary barrier from the left to the right, since the distance they can travel is about 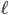 . The ones in box 2 travel from the right to the left are
. The ones in box 2 travel from the right to the left are 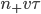 .
. 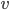 is the average speed. So the net flow rate from box 1 to box 2 is the difference between these divided by the time:
is the average speed. So the net flow rate from box 1 to box 2 is the difference between these divided by the time:
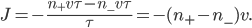
Now, the difference 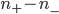 turns out to be approximately the derivative, or the gradient of special molecules, times
turns out to be approximately the derivative, or the gradient of special molecules, times 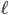 . That is, it's how steeply the number of special molecules drops off per meter. So
. That is, it's how steeply the number of special molecules drops off per meter. So
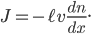
I've actually fudged the derivation by not considering that the molecules can travel at all angles. That would have given me an extra factor of 1/3 out front. But it adds significant complexity for very little improvement of understanding.
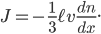
Let us call the factor 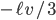 the diffusion coefficient, with symbol
the diffusion coefficient, with symbol 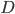 . Then
. Then
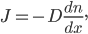
which is quite tidy. You can look up the diffusion coefficient for air, which is about 0.2 cm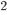 /s. (You could also calculate it by evaluating
/s. (You could also calculate it by evaluating 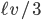 with the mean free path and mean velocity of a gas, but it's simpler and more accurate to just look it up).
with the mean free path and mean velocity of a gas, but it's simpler and more accurate to just look it up).
To figure out how long it will take the special buttery molecules to travel the 10 m length of the hallway, we can make 100 million little boxes of width 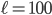 nm. Initially, the far left boxes will have the microwave that has all of that wonderful aromatic special molecules, and the far right boxes have my nose and no special molecules. The density that a person can smell and recognize a molecule is about 0.1-10 parts per million, and a strong smell is about 10-50 parts per million. So the question is, if there's a strong smell initially of 50 ppm in boxes 1 through 5,000,000 (where the microwave is), when does the density get up to 0.1 ppm in box 100,000,000? Because that's when I'll smell it.
nm. Initially, the far left boxes will have the microwave that has all of that wonderful aromatic special molecules, and the far right boxes have my nose and no special molecules. The density that a person can smell and recognize a molecule is about 0.1-10 parts per million, and a strong smell is about 10-50 parts per million. So the question is, if there's a strong smell initially of 50 ppm in boxes 1 through 5,000,000 (where the microwave is), when does the density get up to 0.1 ppm in box 100,000,000? Because that's when I'll smell it.
We can have a computer do this for us. What you have to do is go to each box, calculate the difference in concentration between the adjacent boxes, plug that into 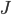 , and then transfer the molecules. But this calculation will take too long, even on a modern computer. So, we'd do better to cut down the number of boxes to something sensible, like 100. The distance is 10 m, so each box will represent 10 cm. Box 1 has
, and then transfer the molecules. But this calculation will take too long, even on a modern computer. So, we'd do better to cut down the number of boxes to something sensible, like 100. The distance is 10 m, so each box will represent 10 cm. Box 1 has 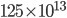 buttery particles per cubic centimeter at the beginning. We'll assume that the popcorn keeps releasing buttery molecules and maintains box 1 at
buttery particles per cubic centimeter at the beginning. We'll assume that the popcorn keeps releasing buttery molecules and maintains box 1 at 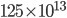 molecules per cubic centimeter. After 1 full second, you see the distribution of buttery particles looks like this:
molecules per cubic centimeter. After 1 full second, you see the distribution of buttery particles looks like this:
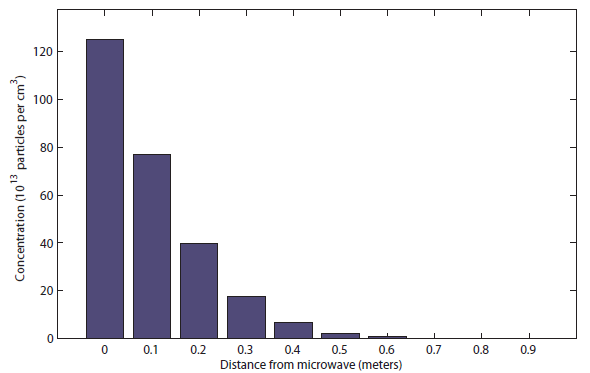 You can see that the popcorn can be smelled only at about half a meter (charitably) after 1 second. Meanwhile, the sound took only about 20 milliseconds to reach all the way to the bedroom! After 10 s, it the distribution looks like
You can see that the popcorn can be smelled only at about half a meter (charitably) after 1 second. Meanwhile, the sound took only about 20 milliseconds to reach all the way to the bedroom! After 10 s, it the distribution looks like 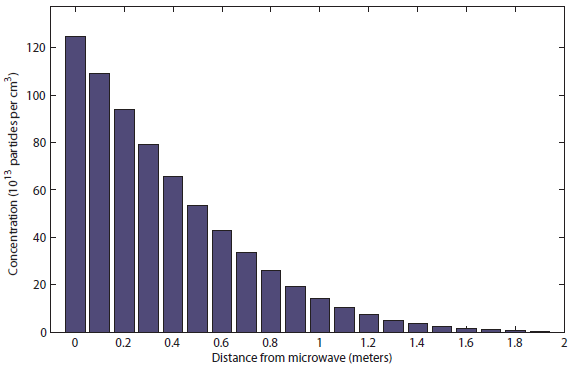 I would say this was probably be distinguishable at about 1.5 meters. Finally, after 100 s (almost 2 minutes), it looks like this:
I would say this was probably be distinguishable at about 1.5 meters. Finally, after 100 s (almost 2 minutes), it looks like this:
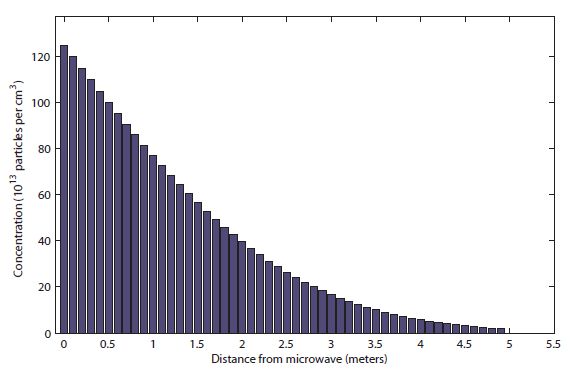 This can be smelled at about 5 meters, halfway to the bedroom. So roughly 5 minutes is totally reasonable! It takes a very long time for particles to diffuse in a gas.
This can be smelled at about 5 meters, halfway to the bedroom. So roughly 5 minutes is totally reasonable! It takes a very long time for particles to diffuse in a gas.
So now let's turn to the sound. Once the microwave starts making noise, it's pushing the air molecules next to it. Those molecules are pushed into a smaller volume and create a local high-pressure system. They then collide with the ones near them along the same direction as they were pushed initially. The collision doesn't take very long at all, since they collide many many times a second. But what traveled down the hallway was not air. Nearly all of the gas stayed in the kitchen. What was moving was a propagating wave of air pressure. If you could look at the air while the sound was traveling, you'd see a pattern of high pressure and low pressure air in between the microwave and my ear. It was this pattern of compressions that traveled to my eardrum and vibrated it, which sent an electrical signal to my brain that there was noise. The equilibrium pressure is normal atmospheric pressure, 101 kPa (or 1 atmosphere, or 760 torr, or 14.7 PSI ...). It looks something like this:
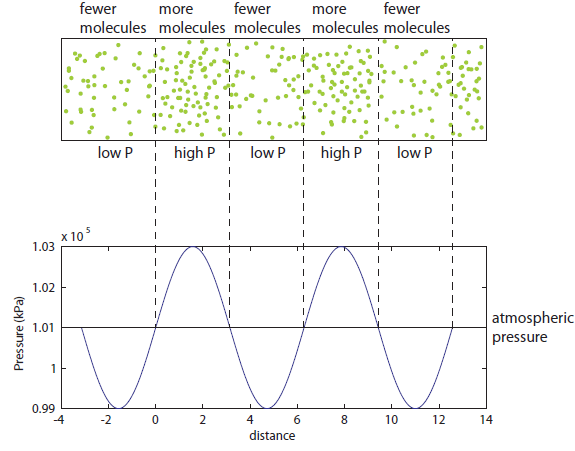 This is what the wave looks like in real space (what you would see if you could see gas molecules). The wave shown could be propagating to the left or to the right. Where the wave has peaks, the pressure is high and the molecules are crowded together. Where the wave has troughs (low points), the pressure is low and the molecules are farther away from each other than normal. If the wave repeats itself in space, the distance between peaks is the wavelength. For this wave, the wavelength looks to be about 6 meters, which would be a 56 Hertz sound (this is close to the lowest A on a piano).
This is what the wave looks like in real space (what you would see if you could see gas molecules). The wave shown could be propagating to the left or to the right. Where the wave has peaks, the pressure is high and the molecules are crowded together. Where the wave has troughs (low points), the pressure is low and the molecules are farther away from each other than normal. If the wave repeats itself in space, the distance between peaks is the wavelength. For this wave, the wavelength looks to be about 6 meters, which would be a 56 Hertz sound (this is close to the lowest A on a piano).
In the figure, you can see that there are imaginary boxes of high and low pressure. What if the boxes were so small that their length was only 1 mean free path? Then the molecules in the high pressure boxes would jump out spontaneously to the low pressure ones in a time 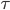 , and the sound would not propagate, because those molecules didn't shove the ones in the low pressure box enough to keep a wave going. Thus, the possible wavelengths of sound are ones where the wavelength is much bigger than a mean free path. That's very interesting. What if I reduce the pressure in the room so that the mean free path gets bigger? What if I decrease the pressure until the mean free path is 1 cm. That happens at about 10 milli-torr (1.333 kPa). Then there is no sound! In a vacuum, such as outer space or the Moon, no sound can propagate. There is some gas there, but it's a much lower pressure than 1.333 kPa, so no audible sound will propagate.
, and the sound would not propagate, because those molecules didn't shove the ones in the low pressure box enough to keep a wave going. Thus, the possible wavelengths of sound are ones where the wavelength is much bigger than a mean free path. That's very interesting. What if I reduce the pressure in the room so that the mean free path gets bigger? What if I decrease the pressure until the mean free path is 1 cm. That happens at about 10 milli-torr (1.333 kPa). Then there is no sound! In a vacuum, such as outer space or the Moon, no sound can propagate. There is some gas there, but it's a much lower pressure than 1.333 kPa, so no audible sound will propagate.
Incidentally, I've way exaggerated the vertical scale on the graph. A difference of 1% from atmospheric pressure would be an ungodly loud noise. A difference in pressure of 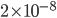 kPa is 60 decibels. That's not deafening, but it's not quiet either. That's incredibly small! A 60 dB noise corresponds to only 20 billionths of a percent change in pressure. The loudness, or intensity, of a sound is given in decibels in terms of the pressure change from atmosphere by
kPa is 60 decibels. That's not deafening, but it's not quiet either. That's incredibly small! A 60 dB noise corresponds to only 20 billionths of a percent change in pressure. The loudness, or intensity, of a sound is given in decibels in terms of the pressure change from atmosphere by
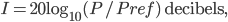
where
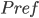 is
is 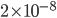 kPa. To give you a feel for that, a whisper is about 0 decibels, and 100 decibels is the threshold of pain. Dogs can bark louder than 100 dB! A normal rock concert is 80-90 decibels. Since it's a logarithmic scale, an increase of 10 decibels is 10 times the loudness.
kPa. To give you a feel for that, a whisper is about 0 decibels, and 100 decibels is the threshold of pain. Dogs can bark louder than 100 dB! A normal rock concert is 80-90 decibels. Since it's a logarithmic scale, an increase of 10 decibels is 10 times the loudness.
We can try to guess what determines the speed of sound in a gas. This gets fairly technical.
The final equation above is called the wave equation. All classical waves---waves on strings, water waves, light, sound---obey this equation. The important part about it, though, is that the factor in front of the
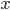 derivative is the speed squared. That is, the speed of sound is
derivative is the speed squared. That is, the speed of sound is 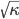 . Luckily, for an ideal gas we can find out what
. Luckily, for an ideal gas we can find out what 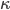 is.
is.We're done! According to this, the speed of sound in air is
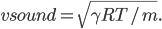
For air,
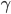 is about 1.4, and the molar mass is 28.97 grams per mole. Using
is about 1.4, and the molar mass is 28.97 grams per mole. Using 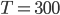 K and
K and 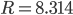 J/K mol, we can get that the speed of sound is 347 m/s. This is pretty good. The actual value is closer to 340 m/s.
J/K mol, we can get that the speed of sound is 347 m/s. This is pretty good. The actual value is closer to 340 m/s.
Note a couple things about this. First, it's off by 2%. You might be fine with that (I usually would be too), but we should always think about where we went wrong. Where we went wrong a little bit is that air does not really act like an ideal gas. The gas molecules are a bit stickier than an ideal gas is. The second thing to note is that sound moves slightly faster in warmer air, which is kind of interesting.
Finally, the speed of sound actually goes up for lighter air (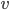 goes up if
goes up if 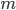 goes down). A cavity's resonant frequency goes up with the speed of sound, so if you breathe in helium, which is lighter than air per mole, you increase the speed of sound, and therefore you increase the resonant frequency of your windpipe. This is why helium makes you sound high pitched.
goes down). A cavity's resonant frequency goes up with the speed of sound, so if you breathe in helium, which is lighter than air per mole, you increase the speed of sound, and therefore you increase the resonant frequency of your windpipe. This is why helium makes you sound high pitched.
In the end, what determines the speed of sound in any medium, not just in air, is how pressure changes with density. That is, if you squish the mass into a smaller space by changing 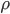 , how much does the pressure change? For a gas, the answer is not that much. You can squish it quite a bit without a giant change in pressure. So the speed of sound is about 340 m/s, which is really pretty slow. But if you squish a liquid down, its pressure goes up by quite a bit. So we expect the speed of sound in water to be faster, and indeed it is (about 5 times faster). And solids are the least squishable, and have an astounding speed of sound 20 times that of the speed in air. The vibration of an oncoming train on its tracks can be felt long before the sound of the train can be heard.
, how much does the pressure change? For a gas, the answer is not that much. You can squish it quite a bit without a giant change in pressure. So the speed of sound is about 340 m/s, which is really pretty slow. But if you squish a liquid down, its pressure goes up by quite a bit. So we expect the speed of sound in water to be faster, and indeed it is (about 5 times faster). And solids are the least squishable, and have an astounding speed of sound 20 times that of the speed in air. The vibration of an oncoming train on its tracks can be felt long before the sound of the train can be heard.