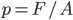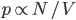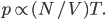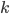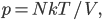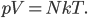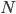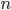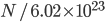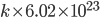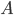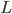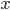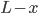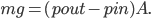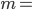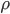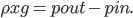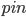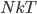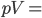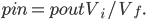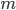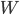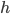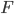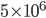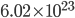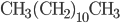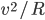Idle Analytics

Thermo for Normals is a short book (~100 pages) I wrote that conveys the basics of thermodynamics without all of the mathematical complexity. Over the next year I will be posting 1 or 2 sections of the text per week. I don't know whether I will ever try to publish it in any other form, though perhaps as an Amazon e-book it wouldn't be a bad idea. Questions, comments, criticisms, and corrections are welcome.

Evaporation and boiling

Drying puddles

If water boils at 212°F, which is when the liquid to gas transition happens, then how is it that a puddle can ever dry up? Surely the temperature is nowhere near boiling, yet large puddles can evaporate over a matter of hours.

The reason is that the molecules in the liquid aren't all going the same speed. Some of them are going faster and some are going slower. Some of the ones going faster have enough oomph to jump right out of the liquid if they're near the surface. After this happens, the liquid has a slightly lower temperature. This is because the temperature corresponds to the average energy per particle. And if the fastest particles leave, surely the average goes down. So the puddle is a little cooler, but it can absorb heat from the ground to put it back at room temperature. Then the process repeats.

Boiling the water, however, is way a much faster way of evaporating it. One you reach 212°F, any more heat added will go directly into particles escaping the fluid.

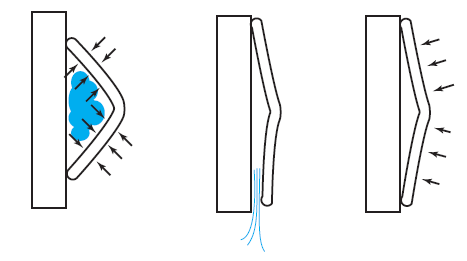
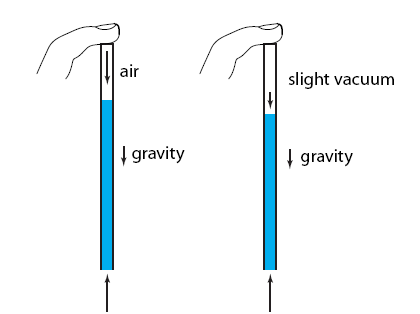
But what exactly is it that these particles have to overcome? Why do some of the particles need enough oomph to get out? What's stopping them? When the water is sitting in the atmosphere, it's constantly being bombarded by air molecules. So, at 212°F you can think that many particles have enough energy to overcome the pressure that the air is exerting, and at room temperature relatively few of them have that much energy. This poses an interesting question: if you reduce the air pressure, is it easier for the water to boil? Yes! In Denver, where the air is "lighter" (actually lower pressure), the boiling point is around 10°F lower than at sea level. This also means that the highest temperature that liquid water can be in Colorado is 202°F, to the consternation of tea drinkers, who insist that the water has to be warmer than that to brew a good cup. They could fix this by finding a way to add pressure to the gas above the water, which is what a pressure cooker does. In fact, in a pressure cooker the temperature of the liquid can be almost as hot as you want it to be. But I doubt we'll be seeing expatriate Brits brewing tea in a pressure cooker anytime soon.

By the way, there's another cool effect that can happen when going to Denver. Bags of chips are packaged at around sea level, which means that inside the sealed bag there is 14.7 psi of air. When being transported to Denver, where the pressure is significantly lower, the air inside the bag will push harder than the air outside the bag, which makes the bags inflate to their limit. Bags are reported to pop open spontaneously when being transported. My guess is that the chip makers have strengthened their bags to prevent this. Over time, tiny leaks in the bags make the pressure equilibrate so that they go back down to normal inflation. So if you're looking for fresh chips in Denver, check for the bags that look ready to pop, because they still have the sea-level pressure of gas in them.

Dying in space

How long can you live in outer space without a space suit? We've seen this in movies before. In the (terrible) movie Mission to Mars, for instance, the character of Woody takes off his helmet while in space and instantly freezes. And this is pretty close to what would actually happen. The absence of any air would make the water molecules in your body have little barrier to jumping out of your skin. All of the fast molecules will rapidly leave, taking away with them most of your thermal energy and causing a sudden catastrophic reduction in temperature.

Superheating

It is actually possible, though difficult, to heat liquid water above its boiling point even without applying pressure. The easiest way to do this is with a microwave and a glass bottle that has a relatively small neck. The molecules down in the fluid would love nothing more than to move to the surface and jump out. To do this they have to combine with other vaporized particles to form the bubble. But the bubble itself is a little hard for them to form; it takes a bit of energy to overcome the surface tension. In my high school chemistry class, they gave us a little rock to put into the water to help this start happening. It's because near the surface of the rock, the energy needed to form the bubble is reduced. But more often, the energy to form the bubble is provided by a mechanical shock, such as stirring the fluid.

If you can keep the fluid very still, the vapor molecules will be unable to form large enough bubbles to percolate out, and the rolling boil you're used to won't occur. But give the  bottle just a little tap and the water will instantly flash boil!

Condensation and vaporization

When you take a hot shower, the room gets steamy (unless it's well ventilated). This does not happen with a cold shower, or even with a not-so-hot shower. With the description I gave earlier, it's fairly easy to understand why. Higher temperature means more water molecules can jump out of the liquid into the vapor phase. And then the mirror gets "steamy", which is water vapor condensing back into liquid, as tiny droplets, on it. This happens because the mirror is relatively cool compared to the air in the room. Water also condenses on the cool walls and ceiling, but it isn't as easy to see.

If you want to clear the mirror, you could wipe it down, or you could use a hair dryer. The hair dryer warms the water that has condensed up and so it re-evaporates (this tends to happen quickly, since hair dryers get ungodly hot).

The same thing happens inside a car. Humans secrete a fair amount of water vapor by breathing, and it tends to accumulate on the nearest cool surface, like the windshield. Now, here's something interesting. When you run the defroster, it doesn't seem to matter whether you use hot air or cold air; it will clear the condensation either way. How can cool air get rid of condensation?

Typical car ventilation systems allow for hot, cold, recirculating, or fresh air, with or without the AC on. You first might notice that the defroster does not work when using recirculating air with no AC unless the air is quite hot. All you're doing is moving the air around. But when the AC function is on, or when fresh air is coming in, the air passing over the glass is drier than the air in the car. What happened with the AC off is that the condensed liquid came to equilibrium with the water vapor in the air.

This is the same condition that hot coffee reaches within seconds. Water molecules jump into vapor until there are as many molecules jumping out as jumping back in. If you blow on the coffee, you remove the equilibrium and allow more molecules to jump out.

So when you blow air conditioned air over the windshield, you upset the equilibrium and cause water to jump out of the liquid to restore it. This will work with either warm or cold air.

Thermo for Normals is a short book (~100 pages) I wrote that conveys the basics of thermodynamics without all of the mathematical complexity. Over the next year I will be posting 1 or 2 sections of the text per week. I don't know whether I will ever try to publish it in any other form, though perhaps as an Amazon e-book it wouldn't be a bad idea. Questions, comments, criticisms, and corrections are welcome.

Freezing and melting

Next up, we'll try to get a handle on some phase changes, when something changes from one phase (gas, liquid, or solid) into another.

First, we should state what is meant by each phase.

A gas is matter where the molecules are flying around in all different directions. And they're flying really fast, about 380,000 miles per hour at room temperature. This is so fast that when you look at the trajectory they take, gravity hardly matters at all. Because of that, when you fill a container with a gas, there are just as many atoms near the top as near the bottom. A gas fills a container that it is put into completely. That implies that the gas can take on any volume that it is allowed to by the vessel it's in.

A liquid has molecules going more slowly that in the gas, though not that much slower. However, unlike the gas, the molecules bump into each other frequently, and they don't get too far away from each other. Molecules stick together much more than in the gas. A liquid will conform to a container that you put it in, but in a way so that it keeps the same volume of liquid. You can't really compress a liquid very much, nor can you expand it. If you have a liter of water you have a liter of water. That's not true of a gas.

A solid has atoms that are packed very closely, much more closely than either liquid or gas. Atoms are directly bonded to each other, and one atom cannot move without the adjacent one feeling it almost immediately. A solid will not fill a container in any way; it retains its overall shape unless the atoms are physically detached from each other by cutting or melting. And just like a liquid, volume never changes.

We are all familiar with the phases of water, H₂O. In gaseous form we call it water vapor. In liquid form it's just water, and in solid form it's ice (this is how I'll refer to them from now on). Ice forms at 32°F (0°C) and vapor is formed at 212°F (100°C). Does this mean that if you have H₂O at 32°F you necessarily have ice? No!

Here's why. Suppose you start out with some liquid at room temperature, and begin cooling it by removing heat in a refrigerator. Every time you remove some heat, the temperature falls. That is, until it just reaches 32°F. At that point you still have liquid. No ice forms. But, if you remove any more heat from the liquid, you don't decrease the temperature. Liquid water cannot exist below 32°F*. So any heat you remove instead makes ice form. If you remove a small amount of heat you create a small amount of ice, and the temperature remains 32°F for both the liquid and the ice crystals. Then you remove some more heat and more ice forms. Again, temperature does not fall. This continues until all the liquid has become ice. After that, removing heat resumes lowering the temperature, and ice can exist in principle all the way down to absolute zero.

This works the other way too. If you start out with warm ice tea and put an ice cube or 3 into it, what temperature is the liquid after a minute or so? 32°F! Why? Because heat will flow out of the liquid into the ice until the ice gets to 32°F (it's usually colder when it comes out of your ice box), and then any more heat you put into the ice cube doesn't change its temperature. It stays at 32°F unless it all melts. And the tea won't stop heating the ice until its temperature matches the ice. So, any fluid with ice in it, after mixing it and waiting a bit, is at 32°F. Putting in a whole lot of ice does two things only: 1. It makes the drink get to ice cold temperature faster and more uniformly (because the ice piles up and can cool the liquid near the bottom, as opposed to just a few ice cubes which will all float and only cool the top part of the drink). 2. It will keep the drink colder longer. Why? Because after it gets to 32°F, you let it sit, and heat begins to leak into the cup from the room. This heat would warm up the drink, but instead the liquid dumps any heat that leaks into it into the ice cubes instead of absorbing it itself. Only once all the ice melts will your drink start to warm up. What adding a lot of ice emphatically does not do is lower the temperature! It's stuck at 32°F, no matter how much ice you add.

At the same time that all of this is happening, though, water molecules from the ice cube are becoming liquid. So, of course, if you leave your drink with a lot of ice in it until half the ice melts, you get the pleasure of a drink that is still ice cold, but is also waterier than before.

The "desire" of substances to change phase is sometimes amazing. When water freezes into ice, it actually expands, taking up more volume in the solid phase than liquid. But what happens if the water is in a container that constricts its volume? The drive to expand is humongous. So, more than likely the container holding the water will explode! You can demonstrate this quite easily by putting a can of soda into the freezer and leaving it for awhile (but be prepared to clean up a mess). Water sitting inside a crack in a rock is capable of actually opening the crack even larger---it literally pulls solid rock apart. Freezing water can break pipes, tear apart trees, and actually lift the foundation of a house.

Thermo for Normals is a short book (~100 pages) I wrote that conveys the basics of thermodynamics without all of the mathematical complexity. Over the next year I will be posting 1 or 2 sections of the text per week. I don't know whether I will ever try to publish it in any other form, though perhaps as an Amazon e-book it wouldn't be a bad idea. Questions, comments, criticisms, and corrections are welcome.

What is pressure?

Now that we have begun discussing mechanics, I'd like to begin talking about some commonplace (ubiquitous, really) phenomena and how we can understand them just by understanding forces between colliding atoms and such.

Pressure has two meanings to most people. First, it's a purely mechanical pushing, such as applying pressure to a wound to staunch bleeding. When you get right down to it, force is always applied to an area. When you're pushing your shopping cart, the palm of your hand contacts the cart's handle over some area. But what if we made the handle very very thin? What if we made the handle a thin wire? Would you still want to push it? No way! It would tear into your skin. The force didn't change, though. The same force as before is required to get the cart moving at speed. But the area would be drastically reduced, so it would hurt.

It hurts because we've increased the pressure. The same would be true if you made backpack straps too thin; it would be painful to your shoulders, even if the pack wasn't very heavy. Have you seen women in high heels walking on the earth? They sink right into the ground if the heels have a small area, but they don't if they have a wide heel. This isn't because the women in stilettos are heavier, it's because all of the weight is on a tiny area, so the pressure is high. Lying on a bed of nails requires care not because the person is heavy but because he's being held up just by the sharp ends, which are 5000 times less area.

On the other hand, pressure clearly increases if you push harder. If pressure goes up as force increases, and goes down if you increase area, it's reasonable to define pressure as the force divided by the area the force is applied to, . The units of this should then be something like force divided by area. In English units we talk about pounds (force) per square inch (area), or PSI. Like many English units, this is still in use because it produces nice numbers. Atmospheric pressure (which I discuss later) is 14.7 psi; the water pressure in your home plumbing should be from 70 to 100 psi. These are good numbers. The Metric system unit is Newtons per square meter, also called a Pascal. What's wrong with that? Well, atmospheric pressure, instead of being a nice number like 14.7 in psi, is 101,000 Pascals. This isn't so nice.

Now, the other sense of pressure is what is exerted by the air. The entire atmosphere pushes on us in all directions. When you are flying in a plane, the pressure 8 miles up is far too low for people to live in, and so the cabin has to be pressurized, which means that more air is pumped in so that it pushes on you as hard as the atmosphere near the ground does. However, our ability to do this is not perfect, and so your ears still pop during takeoff and landing. The ears are, in fact, the main way people seem to experience pressure of this sort. Swimming to the bottom of an 8 foot pool makes your ears hurt due to the high water pressure, even though the rest of your body probably feels fine.

These two different senses are actually physically quite different, even though their net effect is to exert a force over an area.

The sense of pushing one thing against another to apply pressure works basically the way you would imagine at an atomic scale. The atoms of one object form a sheet that comes into contact with another sheet, and one plane pushes the other. Think about a scrum in Rugby: a line of guys links together and pushes on another line of guys. That's how it works when two solid objects push against each other. (See this video if you don't know what I'm talking about).

The other sense of pressure, like atmospheric pressure, is totally different when we zoom in on it. Suppose we have a bottle of air at atmospheric pressure, and we zoom into one of the walls. Rather than seeing a surface pushing against the bottle, all we see are atoms flying around at high speeds and occasionally crashing into the walls and rebounding. That really doesn't sound like the same thing! In fact, the collision takes place so quickly that the atom barely pushes for any appreciable time. What is happening here?

Gas is a state of matter where the molecules are really not constrained in any way. Think of them as very small, very light billiard balls flying every which way. They crash into each other occasionally, and they crash into the container holding the gas. When they do that, they reflect off of the wall with opposite momentum perpendicular to the surface. Here, then, is the force. Any time momentum changes, an outside force had to be involved.

So, we come to understand that the pressure we feel from the atmosphere is actually an average feeling we have from billions of molecules running into us every second and bouncing off. Think if you had a riot shield and were trying to approach a crowd that was throwing rocks at you. If only a few people are throwing them, then you just get knocked back occasionally. But if there are a lot of rocks coming all the time, from your perspective it just feels like a constant force.

Let's try to see what we can deduce from this. This is a little calculation, but don't be afraid of it; we won't do anything more than basic high school algebra. If this description is right, then what would we have to do to the little billiard balls in a gas to make the pressure go up? Well if there were more of them near the wall crashing into it, that would make it go up. So pressure would go up if particle density went up. Calculating particle density is just dividing the number of atoms in the container by the volume of the container:

( is proportional to )
What else? Well, if they were going faster, they would hit harder. Thus, to increase the pressure we should increase the particle energy. It will turn out that the average energy (or speed) of atoms in a gas is roughly the same as temperature of the gas. So, will go up if goes up:

This says that pressure is proportional to particle density and temperature. To make this proportionality an equation, all it needs is a constant somewhere, which we'll just call :

or

This is called the ideal gas law, and it's one of the most well known results in chemistry. It can be derived in a rigorous way, but this understanding is pretty good. Most gases, as long as they aren't at too high pressures, behave very similar to this law.

Another thing we can start to understand is suction. A suction cup is a device that you press against the wall. At first, the cup will not stay up, since there is as big a pressure inside pushing on the cup as there is on the outside pushing on the cup. As you push it against the wall, the cup compresses down and pushes most of the air out, and after the air leaves the cup seals itself at the edge. Then when released, the volume expands but no new atoms come in. From the ideal gas law you can see that if the number per volume decreases, so does $p$. The pressure inside is lower than the pressure outside. So, inside you have some particles running into the suction cup, but on the other side you have way more. The net effect is to produce a net force toward the wall. Who's pushing? The air is!

The force is area. If the pressure inside is quite small, then it's about 15 pounds for every square inch of area. This is actually a lot! 15 lbs is enough to keep up a significant amount of weight (using friction between the edges of the cup and the wall). If the air on the outside wasn't there, then there would be no net force, as demonstrated in this video. When he sucks enough of the gas out of the jar, there are no longer enough atoms on the outside of the cup to provide a force holding the metal up.

Any time there's a pressure differential on two sides of something, there's a force. If you cover the end of a straw with your finger, then lift the straw out of the drink, the liquid in the straw defies gravity. Why? When you lift it up, the liquid does start to fall. After a short time, though, the volume of air between your finger and the liquid increases, but no atoms come in, so the pressure there decreases. The other side of the liquid is in the normal air. This makes a net force pushing on the liquid up, which balances the force of gravity, and so the water just hangs there.

To clarify, the water is held up against gravity because there are more atoms crashing into the bottom than the top.

If the straw is 6" and we have 4" of water trapped, then the water level only drops 0.010 inches, or about 1/4 of a millimeter. This is a really tiny change! It doesn't take much of a vacuum at all to hold the water up. You'd never notice the change in water level, at least in something like a straw.

Thermo for Normals is a short book (~100 pages) I wrote that conveys the basics of thermodynamics without all of the mathematical complexity. Over the next year I will be posting 1 or 2 sections of the text per week. I don't know whether I will ever try to publish it in any other form, though perhaps as an Amazon e-book it wouldn't be a bad idea. Questions, comments, criticisms, and corrections are welcome.

The conserving universe

Last time we discussed the laws of Isaac Newton, which are true (except for extremely tiny things). However, we almost never use them. The reason for this is that they are intuitively easy to understand for simple things, but hard as hell to understand for real things. So, instead, it's better to talk about energy and momentum, each of which is conserved in a system. That way, problems come down to simple accounting.

The first conservation law is the conservation of energy. It states that

What the heck is a closed system? Draw an imaginary box around something. As long as nothing outside the box does anything to something inside the box, then the stuff in the box is a closed system. Energy is roughly conserved on a pool table, so if you draw a box around the pool table, no energy goes in or out of that box, except for when the cue stick is involved, since that comes from outside the box.

But what the heck is energy? I can't tell you. It's like money. What is money? I can't say. But I can say what money does. You can trade money for goods and services. People who produce a lot (or steal a lot, or who inherit a lot, or who do banking ...) have a lot of it. Here's what energy does: if an object has energy, then it can do work, which means it can give its energy to other things. If it's going fast, it has a lot of energy, and can do a lot of work. We normally talk about an amount of energy in Joules. If you have something creating a Watt of power, it's creating energy of 1 Joule every second.

We only recognize 4 kinds of energy. The first is the energy associated with motion. If a particle is moving, it has kinetic energy. This is equal to , where is its speed and its mass.

Kinetic energy is like cash on hand. You can see the particle has it, and it can spend it immediately by exerting a force on something for awhile, which transfers energy to it.

The second kind of energy is energy stored against a force, called potential energy. Potential energy is like energy the particle is owed. At any time, a mass's potential energy can be converted to (traded in for) kinetic energy (motion), and vice versa. If you lift a weight a distance above the ground and set it on a table, you've given it energy , but it hasn't shown up as motion. It's saved up in the bank. But when the weight falls, it cashes in the energy and starts to move. Some examples of forces that store potential energy are gravity, electromagnetic forces, springs, and elastic forces.

An object can also have negative potential energy, which would mean that the particle owes energy. To get it free you have to give it some energy. We all have negative potential energy because of the Earth: to get free of the Earth someone has to give us a lot of energy (I owe about 4 billion Joules). Note that forces like drag or friction do not have potential energy associated with them.

Thirdly, you can have energy stored in electromagnetic fields in the form of light. This energy too can be converted into other forms of energy. The reason why the Sun or a hot lamp makes you hot is that energy is being delivered to you via the light. Induction stove tops send energy across a gap from the range to the pot via very low frequency (non-visible) light.

Finally, there is mass energy, or energy associated with just existing. The equivalent energy of some mass is given by , when something is standing still. If somehow you create a reaction where the mass changes (it can happen!), then some amount of energy was released. We shall not have occasion to talk about this going forward, since it only happens in nuclear reactions, but it should be listed for completeness.

Now, if the system is not closed, then energy can be put into the system by work done from the outside. Energy can also go out of the system if work is done by the system on the outside world. Work is nothing more than pushing over a distance. If you push something with force and it moves a distance in the direction you push, the work you did on it was . This is why energy is measured in units of force times distance. As I said before, it's usually measured in Joules. Other popular units are ergs, calories and BTUs.

The next law is that of conservation of momentum, which holds in any system unless there's an outside force.

Now, if a particle hits a wall, everyone knows that it rebounds, so that its velocity perpendicular to the wall switches direction, meaning momentum is not conserved. The wall, however, is an outside force, so this is fine. Momentum is only conserved among internal collisions. Collisions with the outside means momentum will change.

Now, note something interesting here. Suppose I make my "closed" system, which I'm drawing my box around, be the entire universe. These two laws say that energy and momentum are conserved. That means that the amount of energy in the universe is always the same. However much it started with, it still has that much. Momentum is the same. If you added up all the masses moving to the right times their speeds, you would find it was identical to all the masses moving to the left times their speeds.

That's it for mechanics. We have it out of the way, and can start talking about thermodynamics.

Thermo for Normals is a short book (~100 pages) I wrote that conveys the basics of thermodynamics without all of the mathematical complexity. Over the next year I will be posting 1 or 2 sections of the text per week. I don't know whether I will ever try to publish it in any other form, though perhaps as an Amazon e-book it wouldn't be a bad idea. Questions, comments, criticisms, and corrections are welcome.

Introduction

Thermodynamics is the one topic in physics that everyone should know. Our world is filled with thermal phenomena, from the air we breathe, whirring fans in our computers, the passing of high pressure weather systems, or just the simple act of putting cream into a cup of coffee. Engines, generators, refrigeration, and the like drove the industrialization of the world in the past century. And we now face the calamity of a warming planet, driven by a marginal increasing imbalance of heat from the Sun and Earth's ability to get rid of it.

People don't seem very interested in this topic. It doesn't make it into Star Trek episodes or into popular non-fiction books like A Brief History of Time. This could be because people just don't see the need to analyze things that are perceived to be commonplace—ordinary. Water boils when you apply heat for long enough. It's cold in the mountains. So what?

And yet, all physics is thermodynamics! Any phenomenon of interest in the real world is one made up of a huge amount of particles. Saying something meaningful about this is to describe our universe. If physical laws are the way the chess pieces move, thermodynamics is the game of chess itself.

I think that many people probably think that thermo is a hard topic. In reality, all physics is hard if you try to get all the details right; the universe is ugly, messy, and complicated. But lots of people learn, in either high school or college, the introductory mechanics material. Can they do everything? No. But they can learn something about the world. They cover the 3 laws of motion, the conservation laws, and then do some problems to see where these laws come into play in the real world.

Most people can name 2 out of 3 of Newton's Laws. Most people cannot name a single one of the laws of thermodynamics in any form.

And the fact of it is that you already know a lot about thermodynamics. Though you may not realize it immediately. And this is a huge benefit: most of physics depends on intuition about what should happen. After that, you just need to apply that intuition to work out the quantities. (This is why quantum mechanics is so hard...none of us has any intuition about that!)

This is not meant to be "Thermodynamics for Dummies". I don't think a dummy can learn thermo. I do think that anyone with a Bachelor's degree can, and probably a lot of people with a high school diploma too. The level of physics knowledge required to read the main body of this series will be minimal. A 1 year high school course or a one term college class is more than enough.

Now about math. First of all, I want to make clear that all the math is my job. At no point do you need to reason your way through some math to understand something. You don't even necessarily have to follow along. In fact, I've sectioned off all of it in boxes like this:

If you don't want to read it, don't! These calculations are as simple as they can be, but they are honest physics calculations, and therefore do contain some calculus.

Now, that said, sometimes the easiest way to say something is to show an equation. Imagine if every time I wanted to say I had to say "well, we know that force equals mass times acceleration". As long as you can recognize what the operations of addition, subtraction, multiplication, division, and taking something to a power, you'll be fine. You should be familiar with these things, though:

• How to read a graph, or a chart
• numbers expressed in scientific notation, or as a number times a power of 10
• What a unit of measurement is

If you know what a chart means, if you understand is 5 million, and if you know what a meter is, you'll be alright.

This series will proceed as follows. First we'll review the laws of mechanics, including Newton's laws of motion, energy conservation, and momentum conservation. That's how the chess pieces move. Next, we'll take a look at some common thermodynamic phenomena that can be understood with only this basic mechanics understanding. After that, we'll come to the 3 laws of thermodynamics themselves, delving into their consequences.

Here are some phenomena that I'd like to address. It is not comprehensive, but just a few examples:

• Why do puddles dry up if they aren't boiling?
• How do you make "cold"?
• Why is it cold in the mountains?
• Why can't you make good tea in Colorado?
• Should you leave the heat on when you leave the house?
• How energy efficient can cars be made?
• How does global warming work? Why can't we just air condition the Earth?
• What does thermodynamics suggest about the beginning and end of the universe?

We'll try to learn from the bottom up, starting with things that we all see and know every day, and then getting a bit more technical to try to wrestle with stuff that isn't so commonplace.

List of Terms

Here are some words that we need to bandy about that I do not define elsewhere in the text.

Atoms - The building block of all normal matter. The atom has a very small center, called the nucleus, made up of extremely heavy protons (positively charged) and neutrons (no charge). Surrounding this nucleus are very light, negatively charged particles called electrons.

Macroscopic - Something that's average, everyday life-sized. Air in the room, baseballs, bottles of water, these are all macroscopic. By contrast, atoms or the transistors on microchips are microscopic.

Moles - A mole is just a word that means of something. If you have 1 mole of argon gas, that means you have argon atoms.

Molecule - One or more atoms that are bonded together. Hydrogen gas is molecular because it is almost always , or two hydrogen atoms bonded together to make a molecule. Molecules can have huge numbers of atoms, such as or just one atom like Ar.

Per - This means that you divide. If you have 10 apples and 2 people then you divide 10 by 2 to get the number of apples per person. Per always means that something is divided by something else.

Phase - In thermodynamics, usually refers to whether something is gas, liquid, or solid.

Proportional - If something is proportional to something else, then it scales like it. If I say that the cost of going to the movies is proportional to the number of people going, I mean that if 5 people go it costs 5 times more than if 1 person goes.

Vacuum - Having little to no molecules.

The Laws of Motion

Newtonian mechanics contains the laws that govern how objects move around, collide, speed up, or slow down. This post is intended as a review for those who have seen this material before, but maybe don't think about it all the time. We need to know how the pieces move, but we don't need to know a huge amount of detail about it. It might be readable to someone who hasn't ever taken any physics, but it's a lot of information to absorb all at once.

Laws of nature in general become less intimidating when you realize that your brain has specialized hardware to understand them. Our evolutionary ancestors developed this hardware to stay alive, since they needed to judge how fast something was coming, or how much something would hurt if it fell on them, etc. So, all laws of mechanics, and indeed 2 out of 3 laws of thermodynamics, have a "caveman version". This version is correct but incomplete. The caveman version is the part that is innate, but to get the proper understanding you need to think about it with your rational mind.

What we are concerned about is particles. What the hell is a particle? In principle, it could be anything: atoms, footballs, cars, planets, etc. Any thing where the internal motion of its parts doesn't matter can be called a particle as far as we are concerned (for our purposes, we will normally talk about atoms). Particles have mass. They have charge, though most things we talk about are neutral. They have position, which is to say that they are somewhere. They have velocity, which means that they have a speed and are traveling along some direction. Finally, they have acceleration, which is how the speed and/or direction is changing. If something is standing still its velocity is zero. If it's going along with the same speed in the same direction, its acceleration is zero.

Here's the first law of motion:

If there's a rock sitting on the ground, and nothing acts to move it, then it just stays there. Simple. People say something slightly more technical-sounding: an object at rest tends to stay at rest. That's a fine interpretation.

There is also a common addendum to the above: an object in motion tends to stay in motion. This one caveman probably did not know. For it often seems that objects in motion stop on their own, without anyone having touched them. Even a hockey puck on ice will come to a stop sooner or later. To a modern person, it seems natural that you have to keep your foot on the gas to keep your car moving forward. But this is only because he doesn't realize that the gas applied overcomes drag on the car due to air resistance and internal friction. If those forces weren't there, the car would just go on forever, and you'd never have to apply the gas once you got up to speed. Once one realizes that friction and drag are ever-present on Earth, the First law is obvious. However, I assure you that many undergrad college students assert that there is a force of motion that keeps things going. No such thing exists. Things that are moving keep on moving with no forces applied. They only stop if something acts on them.

The full and accurate statement of the First Law is this:

The converse is true. If something does not travel in a straight line with constant speed, then there must be forces on it. Note that being at rest means speed is 0, and so in absence of force speed stays 0, and the caveman form is true. Note also that if something travels in a circle at the same speed, it still has acceleration since its direction is changing (the acceleration is the famous centripetal acceleration, which every intro course student is subjected to).

Next up is the Second Law:

Let's unpack this. First, it's not clear what heavy means. If something is heavy, that means that it's hard to lift the object upwards against gravity. And it so happens that things that are hard to lift are also hard to push horizontally, but not always as hard.

This gets at two things at once really. An object has a property—mass—that can't really be explained in terms of other things; it's just mass. And gravity pulls proportionately on massive objects. If something has twice as much mass as another thing, that means it's twice as hard to lift. It also means that it has twice as much friction between it and the ground. And, finally, it means that even if it's on wheels (so that friction is irrelevant), it's twice as hard to get moving. Think of pushing a refrigerator on wheels—just because there's no friction doesn't mean it's a cinch to get going at speed.

In technical terms we would talk about acceleration, which is nothing more than how quickly something picks up speed along a given direction. We say that for a given push , we accelerate an object with mass by an amount along the direction we push. If you push twice as hard, the acceleration is twice as big. If the mass is twice as big, you only get half as much acceleration from the same push.

Of course, what we mean is total force. If an object is acted on from the right and the left equally, these forces cancel so that acceleration is zero. Also, we didn't say what happens if the mass changes. But no matter, the above is good enough for our purposes. So here's a decent statement:

Finally, we have the third law, whose caveman version would be something like "I can punch hard, but when I do my hand hurts!" If something, like a fist, exerts a force on another object (say, Bob's face) then the other object also pushes back with the same force. You can punch a face, but the face also punches your hand with the same force. If you break his face, you might break your hand. In common parlance, for every action there is an equal and opposite reaction.

This can be illustrated in the case of a collision in billiards. If the 13 ball is moving to the right, and the 8 ball stationary, then in the collision the 13 ball will push on the 8 ball, and the 8 ball also pushes on the 13 ball in the opposite direction, with exactly the same force.

The above laws are great for getting a feel for real world problems. However, the two conservation laws are, while more abstract, truer than those above, since there is no known exception to either of them (Newton's laws break down quite easily in the quantum world, and the third law is invalidated even without quantum mechanics). I leave those until the next post.