A simple elimination algorithm that searches box-by-box, row or column will solve most Gentle and maybe even some Moderate puzzles. The final simple technique knocks out pretty much any remaining Gentle:
Technique 4: Enumeration
If the previous searches fail, try checking each square on an individual basis to see what numbers it can "see". For each square run through the numbers 1 through 9. You may find that a given square sees every number but one of them.
This doesn't really need its own example. I've used the word "see", which is common, to indicate that the square you're looking in is in the same box, row, or column as the number of interest. That is, a number that excludes a possibility is something the square can see. Enumeration looks at a square and its relation to all three groups (box, row, and column), starting with the premise that "well, some number has to go in this box".
Technique 5: Indirect inferences
The key to solving every Sudoku is to make the logical inferences required by the basic rules, obviously. But the complexity of these inferences goes up with the difficulty. The techniques used by advanced players reduce the complexity to a simple and recognizable pattern that can be searched for.
Consider the following puzzle:
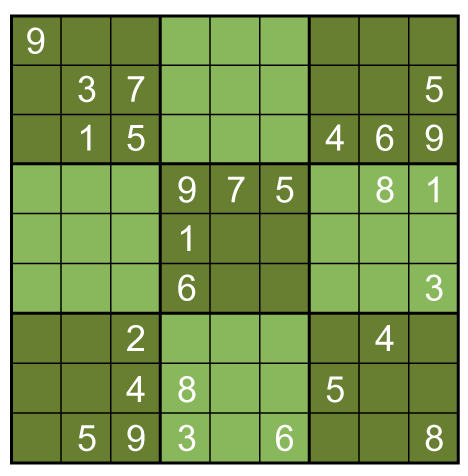
Focus on Box 4 (far left box in the middle row of boxes). What do we know about where the 1 goes? The 1 from the box above it means that it's not in column 2, and the 1s to its right mean that it is either in square 7 or square 9. But now look at Box 7 (far left box in the bottom row of boxes). The 1 in Box 1 excludes the 1 from being in the middle row, but it could be in any one of the squares in the left column. But it has to be in the left column! So we know that the 1 in Box 4 must be in square 9: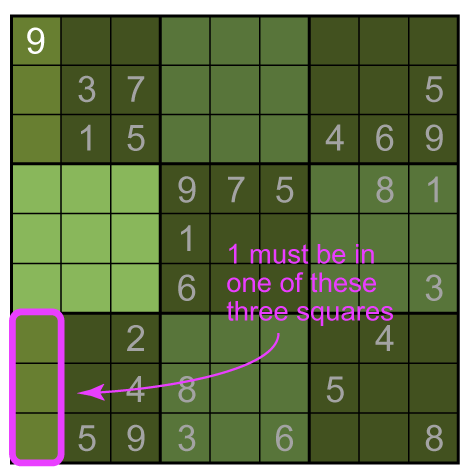
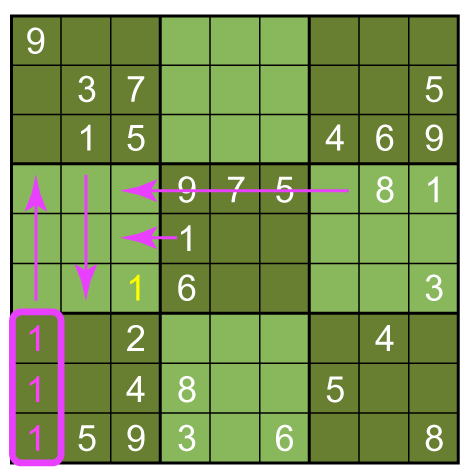
This is an indirect inference. We don't have to know where the 1 is exactly, we only have to know where it is in relation to the box we're interested in. The same works for the 3, if we notice two simultaneous indirect inferences: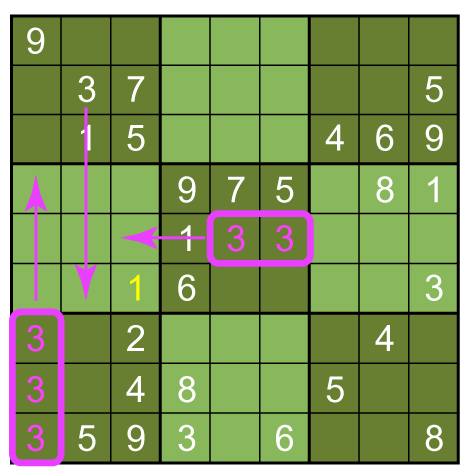
The 3 in Box 1 means that 3 appears in the left column of Box 7, and the 3 in Box 6 means that a 3 occurs in the middle row of Box 5. Thus the 3 in Box 4 must be in square 3. These two solves are not possible without this kind of inference. And, fair warning, this does come up in Gentle puzzles (though not usually two simultaneous ones like the latter example).
Implementing this kind of reasoning in your head takes a bit of practice. While I'm doing a basic search pattern, I note any such grouping that puts a number in a row or column without knowing exactly where it is. If I see one, I quickly look at adjacent boxes to see if that helps solve something. If not, I leave it. Once you've done it enough times, it isn't hard. Just remember that you can know something about the placement of a number without knowing everything about it.
Pencil Marks
Once a puzzle gets above Moderate, and sometimes even Moderate itself, you'll sometimes want to start listing the possible candidates for a given square in the square itself. These are called "pencil marks", since obviously you'll want to erase them later. So, continuing the puzzle above, I solve for a couple more numbers, and then I list in Box 9 the possible candidates for some of the remaining squares:
For a puzzle that's not too complex, it isn't worth going through and doing the pencil marks for every square. The pencil marks help us cut down on the amount of complexity we have to do mentally. They can, if you will, "store" a large number of inferences we've made that are hard to remember all at the same time. In this way, we break the problem down into smaller parts. For now, I'd rather not explain why I did the pencil marks in these specific squares (I do have some guidelines for when to do so, but let's leave it for later). Listing the pencil marks is as simple as carrying out Enumeration. Instead of mentally running through the numbers, you list any number that isn't excluded (any number that isn't seen by the square).
Now, in the figure above, look at the bottom row. The 2 in the bottom row has to appear in the seventh or eighth squares (Box 9 square 7 or Box 9 square 8). Thus, it cannot occur in Box 9 square 6. We have that listed as a possible candidate, but we can now remove it from there:
Notice that in the far right column, two of the squares have their candidates listed as 6 7. Those squares can only be 6 or 7. If one is a 6, the other is a 7, for sure. That means that the square at the top of this column cannot be 6 or 7. We have found a twin.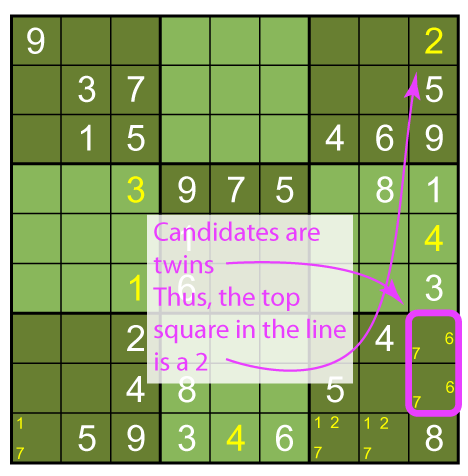
In this case, it would normally be called a naked twin, because you can just look and see it plainly. As we'll see, this isn't always so. Now, the 6 7 twin also allows us to remove 7 as possible candidates from the other squares in Box 9, because those cannot possibly be 7 either:
From this, we see that we have another twin, 1 2 in the bottom row. This forces the far left square in the bottom row to be 7, since 1 must be removed.
Now, to find the naked twin, we had to notice that the 2 was required to be in the bottom row of Box 9. In fact, the squares in the bottom row in that step all had possibilities 1 2 7. The left-most square had 2 excluded, but nonetheless the pencil marks match if we ignore that. This is also a twin (or a triplet, if you like). However, it is a hidden twin, in that you can't just tell at a glance that it is a twin. The inference that the two had to be in the bottom row of Box 9 needn't have come from recognizing the triplet. Such an observation is a kind you can make any time, and it won't necessarily correspond to any of the common techniques.
With this in place, the puzzle can now be solved with basic methods already discussed. The answer is below.
Now, back to pencil marks. If I think a puzzle is "hard" (as in unyielding), I will normally start filling in pencil marks. As you can see from the above, I had gotten all the way through the three major search patterns and only come up with four solves---and two of those required an indirect inference! So, when I see that, I just resign myself that this one is going to be a bit tough and start listing. A good place to start listing is where you see a given box intersects a lot of different numbers. When you try Enumeration on it, you will get only two or three candidates. And then, obviously, you want to search for twins, so do the pencil marks on adjacent squares. This is how I came to list the pencil marks you saw above. Had I not started there, the puzzle might have taken a bit longer.





