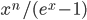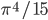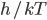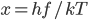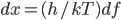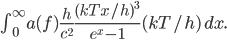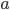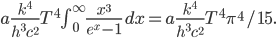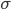Now we know the amount of radiation coming from an object with a surface at temperature 
. And we know the amount for each frequency of light. It's
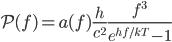
where
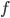is frequency you're interested in, 
is the speed of light, and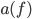 
is a property of the object called emissivity. Emissivity measures the fraction of white light that is emitted and absorbed by the surface, and could be a function of 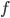if, say, something absorbed blue but not red and green (such an object would be yellow). This equation tells you the energy radiated per time and per surface area in the neighborhood of :
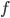\begin{align*}\mathcal{P}(f) \, df = & \text{The amount of energy that leaves a body at temperature $T$} \\
& \text{as radiation at frequency $f$, per second and per square meter}.\end{align*}
(This isn't precise. Technically this only gives you the amount in a small range around 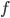, and the only way to get the amount is to integrate. However, that's confusing as hell until you get used to it.) To get the actual amount of energy radiated out of it, you have to add up the values for the frequencies you want to know about, multiply by the surface area of the object, and multiply by the time it radiates for.
But let's assume we just want to know the total amount of all radiation, no matter what frequencies it's composed of. Then we just need to add up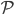 
for every frequency. That will give us the cooling rate for a body with surface temperature due to radiation:
Important!
The total amount of energy radiation per unit area per unit time is
The integral of
is quite difficult, so I'll just quote the result (but see here for the calculation) which is 
. We have to get rid of the 
in the exponential to use this, so let 
, 
. Therefore,
Now, and this is a very important assumption, assume that the emissivity is the same for all frequencies. That is,
is a constant for a given object. Then,
Let's wrap all those constants into a number called
.The total radiation from a body at surface temperature
per time per surface area is, then,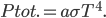
W m
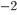K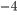
) times 
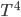, times the emissivity. The temperature is the temp at the surface, which might not be the same as the temperature of the interior! The interior of the Sun is millions of kelvin, but its radiation temperature is 6000 K because that's the temperature of the surface.
If you have an object with surface area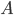 
, then in time 
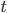it radiates 
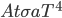of energy. Human skin is an almost perfect emitter in the IR (emissivity is 0.98), and so is clothing for that matter. Assuming that an average person has about 2 square meters of skin, and that skin is 33 °C = 306 K, then the amount of heat radiated every second by a naked person is 1000 J. You are emitting 1000 watts if you're standing around naked. At that rate, you'd be freezing in a very short time! Now, the thing is that the environment around you is radiating back at you as well (unless you're in outer space without a suit ...). If the walls are 20 °C = 293 K, then they radiate an energy per unit area of 
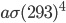, and drywall emissivity is also close to 1. You absorb 
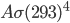of energy every second from your environment. So the net loss is only 
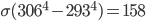watts, or 158 joules every second if you're naked. If you're clothed, then the temperature of the surface is the temperature of clothing, which is more like 28 °C = 301 K. In that case, usually you are losing 95 watts in radiation, enough to power a very bright light bulb (in principle). Of course, I've left out any effects of the other two ways heat gets around: conduction and convection. We come back to that next time, where I'll speak about the way humans experience and perceive heat.
Now think about the Earth. It has no conduction or convection with the rest of the universe, since all that there is outside of the thermosphere is vacuum. The Sun is the same. So the Earth radiates some energy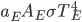 
for its surface temperature 
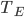, surface area 
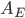, and emissivity 
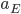; and the Sun emits 
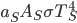for its surface temperature 
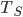and area 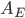. Now, the radiation from the Sun has spread out in all directions, so the energy per area is lower by 
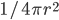, where 
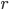is the distance from the Sun. So if we take the distance from the Sun to the Earth to be 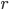, then the amount of radiation the Earth emits is
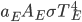
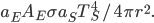
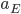is both the fraction emitted and the fraction absorbed, and 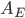is the area that the radiation density 
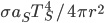is incident on. So long as the Earth's temperature isn't rapidly changing, then these two values must balance. This gives you a small taste of the thermodynamics of climate change, which we'll take up in detail later.
During the calculation, one has to assume that the object emits and absorbs all frequencies at the same rate for all frequencies or light, which is to say that emissivity is just a number. This is not always going to be very accurate. Tungsten, which is used as the filament in light bulbs, has an emissivity that looks like this:
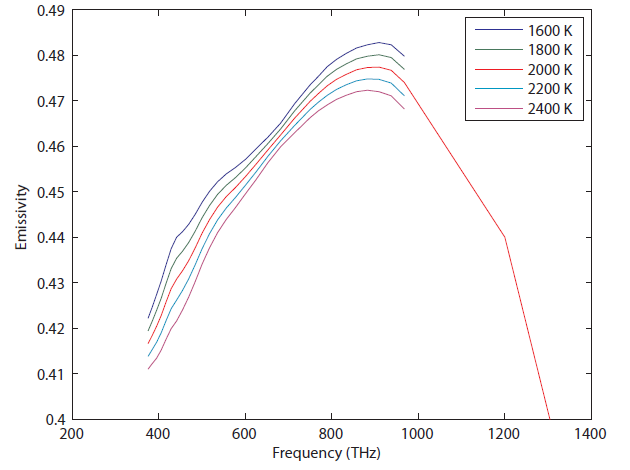
Spectral emissivity of tungsten at high temperatures (from R.D. Larrabee, MIT Technical Report 328 (1957))
You can see that the value for emissivity actually depends not only frequency, but also on temperature. Nevertheless, observe that the vertical axis is not a very big range (from 0.4 to 0.5), so if you were to say that the emissivity of tungsten is about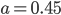 
, you'd be correct within 10%. To do any better, you have to calculate the above numerically, using the data from experiments. The point is, tungsten radiates more at 1000 THz than it does at 400 THz, but not by a huge amount. However, the emissivity for things such as clouds in the atmosphere may be very important, so keep it in mind.