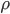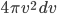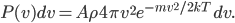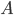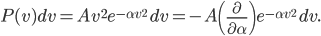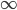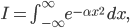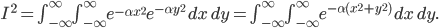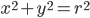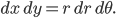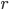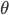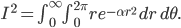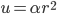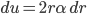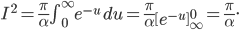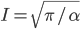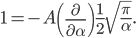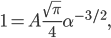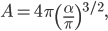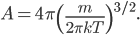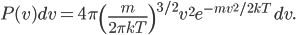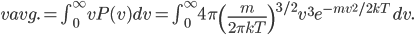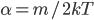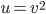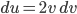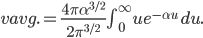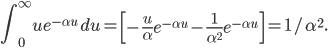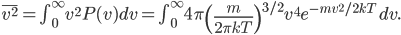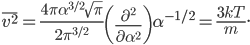A molecule in a gas is being knocked into by lots of surrounding gas molecules. This is a very complex, almost random-seeming process. And yet we know that at higher temperatures the gas molecules simply must be moving faster on average. There must be a relationship between the temperature and the average energy. Moreover, we should be able to get some idea of how fast these molecules are moving.
The molecule is in a gas at temperature  , and so its probability of having energy
, and so its probability of having energy 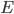 at some time is proportional to
at some time is proportional to 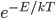 . But let's stop to think about what this means for a minute. The thing is, there are lots of ways to have a given energy
. But let's stop to think about what this means for a minute. The thing is, there are lots of ways to have a given energy 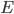 . Suppose we choose
. Suppose we choose  eV. An oxygen molecule would have 1 eV of energy if it was traveling to the right at 2454 meters per second. But it would also have 1 eV if it were traveling to the left at 2454 m/s. If it could only move to the left and right, then, the probability of having 1 eV would have to be counted twice. That's in contrast to having zero energy. There's only one way to have zero energy. We would only count that once.
eV. An oxygen molecule would have 1 eV of energy if it was traveling to the right at 2454 meters per second. But it would also have 1 eV if it were traveling to the left at 2454 m/s. If it could only move to the left and right, then, the probability of having 1 eV would have to be counted twice. That's in contrast to having zero energy. There's only one way to have zero energy. We would only count that once.
Once we let atoms start to move in 3 dimensions, now suddenly there are a lot of ways to have a certain energy. There are a bunch of different angles, all with the same speed, that would have energy 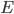 . Even though the probability of having a certain energy is
. Even though the probability of having a certain energy is  , we actually have to add up a bunch of the probabilities for every energy, since there are lots of ways to have a certain energy. That is, except for 0. At 0, there is only one way, no matter how many dimensions there are. So even though the probability initially looked large at
, we actually have to add up a bunch of the probabilities for every energy, since there are lots of ways to have a certain energy. That is, except for 0. At 0, there is only one way, no matter how many dimensions there are. So even though the probability initially looked large at 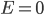 , there's actually only a very small chance of having 0 energy.
, there's actually only a very small chance of having 0 energy.
Now, we can easily change energy into velocity, providing there's no potential energy. Energy is just one-half times mass times the velocity squared. A given particle can travel in all 3 directions, which we call 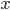 ,
, 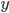 , and
, and 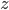 . Then it travels along the
. Then it travels along the 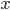 direction with velocity
direction with velocity 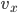 , along
, along 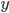 with
with 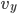 , and along
, and along 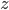 with
with 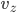 . If
. If 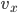 , for instance, is positive, that means it moves to the right, and if
, for instance, is positive, that means it moves to the right, and if 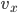 is negative it's moving to the left. The energy is
is negative it's moving to the left. The energy is 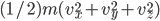 and the speed is
and the speed is 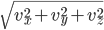 . So now what we want to know is, what is the probability of having speed
. So now what we want to know is, what is the probability of having speed 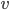 in a gas? (Note: you can read Wikipedia's entry on this if you want. Their derivation is bullshit.)
in a gas? (Note: you can read Wikipedia's entry on this if you want. Their derivation is bullshit.)
To make it simpler, we'll assume that velocity only comes in certain units (this is actually true). And we'll just form a grid and look at it. Here it is drawn in only two dimensions.
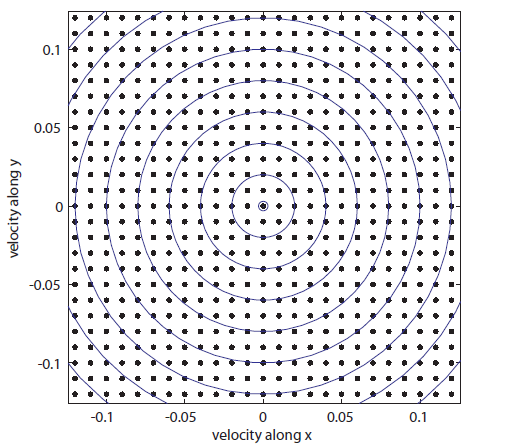 Each point represents a velocity the molecule can have. The one in the very center is
Each point represents a velocity the molecule can have. The one in the very center is 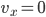 and
and 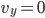 . You can see the tiny circle drawn around it. That circle represents zero speed. And it only holds one point, because, after all, there is only one way to have speed 0: the velocity in each dimension has to be zero. Now, the next circle going out from that is a bigger speed. All of the points enclosed by the next circle, but outside of the first one, are at a slightly higher speed. There are about 8 of them. The probability of having that energy is proportional to
. You can see the tiny circle drawn around it. That circle represents zero speed. And it only holds one point, because, after all, there is only one way to have speed 0: the velocity in each dimension has to be zero. Now, the next circle going out from that is a bigger speed. All of the points enclosed by the next circle, but outside of the first one, are at a slightly higher speed. There are about 8 of them. The probability of having that energy is proportional to 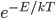 , and
, and 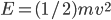 . But that probability applies to every point in there. So the probability of having speed one step above zero goes down because of
. But that probability applies to every point in there. So the probability of having speed one step above zero goes down because of 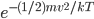 , but goes up because we multiply by 8. Then we increase
, but goes up because we multiply by 8. Then we increase 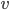 again; that's the third circle. The probability of having that speed is
again; that's the third circle. The probability of having that speed is 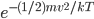 times the number of points in that circle (I count 36). The circles get a bigger radius, and so they form strips of more and more speed/energy every step.
times the number of points in that circle (I count 36). The circles get a bigger radius, and so they form strips of more and more speed/energy every step.
But you might see what's happening. Even though the number of points is going up, the probability 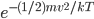 is going down every step.
is going down every step.
So now all we have to do to form the probability of a certain speed is to count the number of points between one circle and the circle inside that, and multiply that by 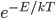 . If I do that for all the speeds (in three dimensions, even though the above graph only shows two), and then divide by the total, I get the probability as a function of
. If I do that for all the speeds (in three dimensions, even though the above graph only shows two), and then divide by the total, I get the probability as a function of 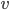 :
:
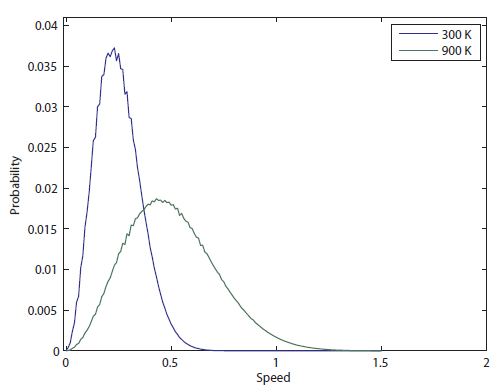 So the probability of having no energy is not a maximum at zero. In fact, it's tiny! Then it rises to a maximum, and then it tails off to the right. At 300 K, the peak is at pretty low energy, and it tails off kind of quickly. At 900 K, though, the peak happens at a higher energy, and there are lots of molecules at higher energies. Duh! Of course, that's what we expect for a gas. If the temperature is higher more atoms are running around faster.
So the probability of having no energy is not a maximum at zero. In fact, it's tiny! Then it rises to a maximum, and then it tails off to the right. At 300 K, the peak is at pretty low energy, and it tails off kind of quickly. At 900 K, though, the peak happens at a higher energy, and there are lots of molecules at higher energies. Duh! Of course, that's what we expect for a gas. If the temperature is higher more atoms are running around faster.
The graph shown above is called the Maxwell-Boltzmann distribution. It tells you, for a gas, how many of the gas molecules have a certain speed, based only on what kind of gas it is (the mass of the molecules) and the temperature. That is a hell of a lot of information from just those two things! Imagine trying to guess how many people made $25,000 per year just by knowing that the country is the United States and the GDP is 12 trillion dollars. How accurate do you think your guess would be?
If I'm going to want to get averages and stuff, we'll want an actual mathematical expression for the distribution, so I'll derive it here. As always, skip past it if you like.
With this, now we can tell all the important statistics of a gas. How fast are the molecules moving on average? We can calculate that! I'll do it later, but the answer is
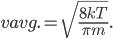
That's it. So, for argon gas at room temperature, the average speed is 398 meters per second, or about 890 miles per hour. Oxygen atoms in the air are traveling about 995 miles per hour. That is damn fast.
What about the average energy? For that we need to find the average of 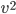 (which we usually write
(which we usually write  . A line over it means "average"). We can calculate that too. The answer is that the average of
. A line over it means "average"). We can calculate that too. The answer is that the average of 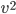 is
is 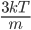 . So the average energy of a gas molecule, so long as it only has kinetic energy, is
. So the average energy of a gas molecule, so long as it only has kinetic energy, is
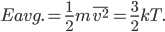
The average energy of a gas molecule in a monatomic gas is just three-halves
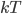 . This will not work for diatomic gases like oxygen or certainly for something like steam. This is because diatomic or polyatomic gases have more ways of having an energy
. This will not work for diatomic gases like oxygen or certainly for something like steam. This is because diatomic or polyatomic gases have more ways of having an energy 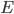 : they have ways to rotate, and the chemical bonds can vibrate. So being at a temperature
: they have ways to rotate, and the chemical bonds can vibrate. So being at a temperature  would imply that there was more energy in the gas. We'll come back to that.
would imply that there was more energy in the gas. We'll come back to that.
Now, a monatomic gas is made up of a lot of atoms, and not all of them have the same energy. But since they have 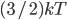 on average, the internal energy of the gas is just the number of gas molecules
on average, the internal energy of the gas is just the number of gas molecules 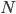 times this, or
times this, or
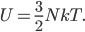
If you look at that, since we know that heat is added as energy, we see that if we want to increase the temperature by 1 K then we have to add
 of heat. That means that, by definition, the heat capacity of a monatomic gas is
of heat. That means that, by definition, the heat capacity of a monatomic gas is  . Let's look at the heat capacities of 1 mole (
. Let's look at the heat capacities of 1 mole (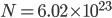 atoms) of some monatomic gases:
atoms) of some monatomic gases:
Heat capacities at constant volume for monatomic gases.
| Gas | 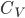 (J/mol K) (J/mol K) |
|---|---|
| He | 12.5 |
| Ar | 12.5 |
| Ne | 12.7 |
| Kr | 12.3 |
And what do we think it should be?
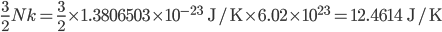
Pretty damn good!
All of this came from one simple result, that (at least for one dimension), the probability that a molecule in a gas at temperature  has energy
has energy 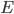 is
is 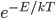 . Everything else was just figuring out how many ways there were to be at that energy, and this told us how the speeds are distributed. It's quite amazing.
. Everything else was just figuring out how many ways there were to be at that energy, and this told us how the speeds are distributed. It's quite amazing.